Switches and transitions

A lot of signals can have anomalies and special events that happen on specific timeframes:

• a promotion gives a temporary boost in sales
• an outage results in a loss of 90% of the data volume
• a device gets broken and generates more noise
• the creation of a new shop adds a new linear trend to the revenue of a company
• a holiday makes a seasonality pattern change

These events can happen in two ways:

• the signal suddenly changes: instant change.
• the signal gradually changes to reach a new value: change with transition period.

In mockseries, this kind of change is called a switch. Let's see how to create such switches, and how to create custom transitions.

Switch and revert

Consider a simple switch: the base value is 0, and it changes to 1 after 2 days.

from datetime import datetime, timedelta

# plotting utilities for the whole tutorial

import matplotlib.pyplot as plt

plt.rcParams["figure.figsize"] = (20,7)

from mockseries.trend import Switch

today_midnight = datetime.combine(datetime.now().date(), datetime.min.time())

switch = Switch(

start_time=today_midnight + timedelta(days=2),

base_value=0,

switch_value=1,

)

switch.preview_week()

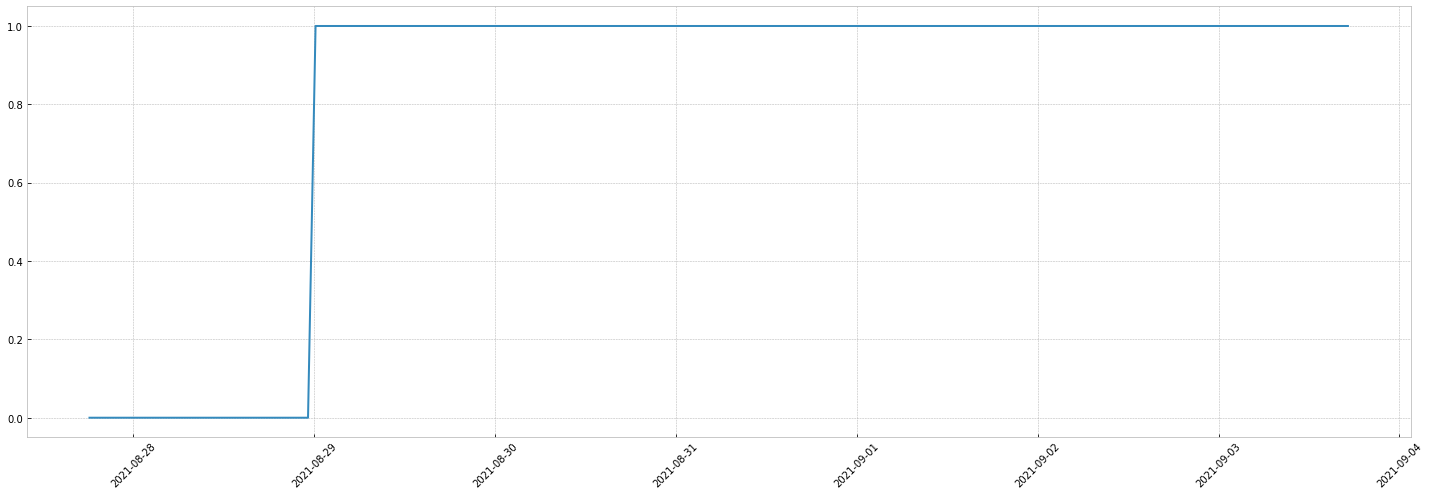
You can configure the switch to revert to the base value.
Let's revert 2 days after the change.

switch_and_revert = Switch(

start_time=today_midnight + timedelta(days=2),

base_value=0,

switch_value=1,

stop_time=today_midnight + timedelta(days=4),

)

switch_and_revert.preview_week()

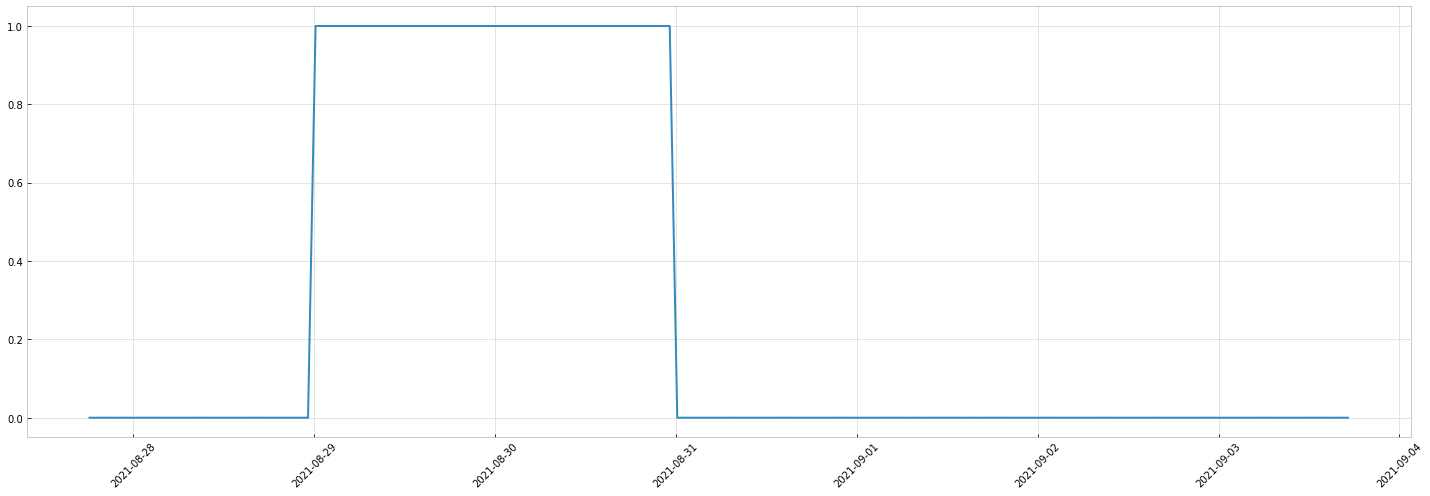
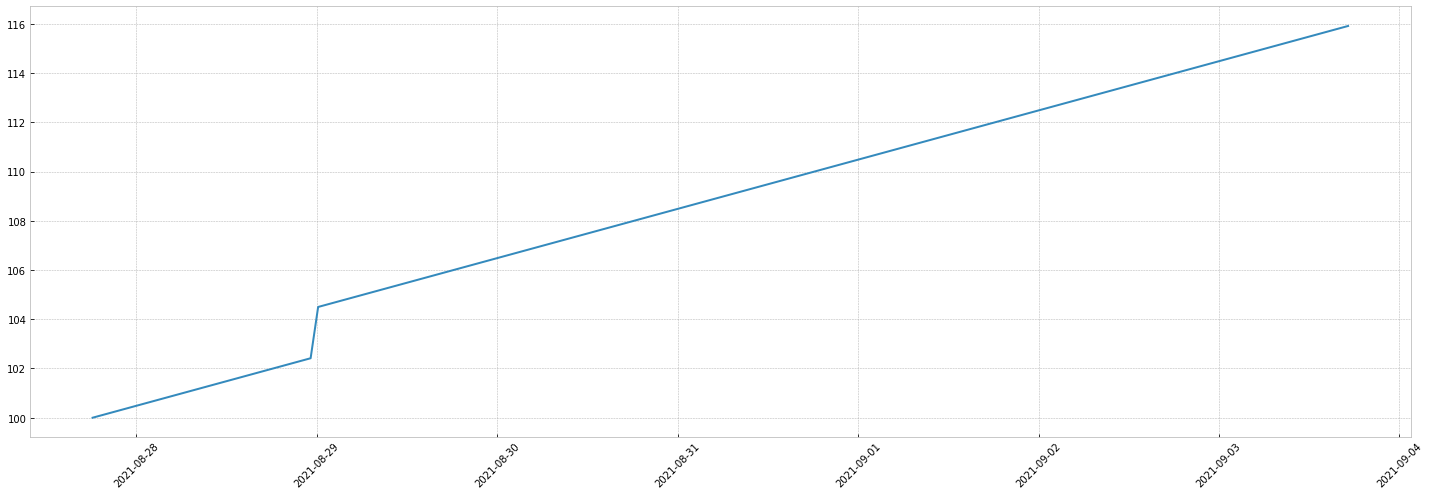
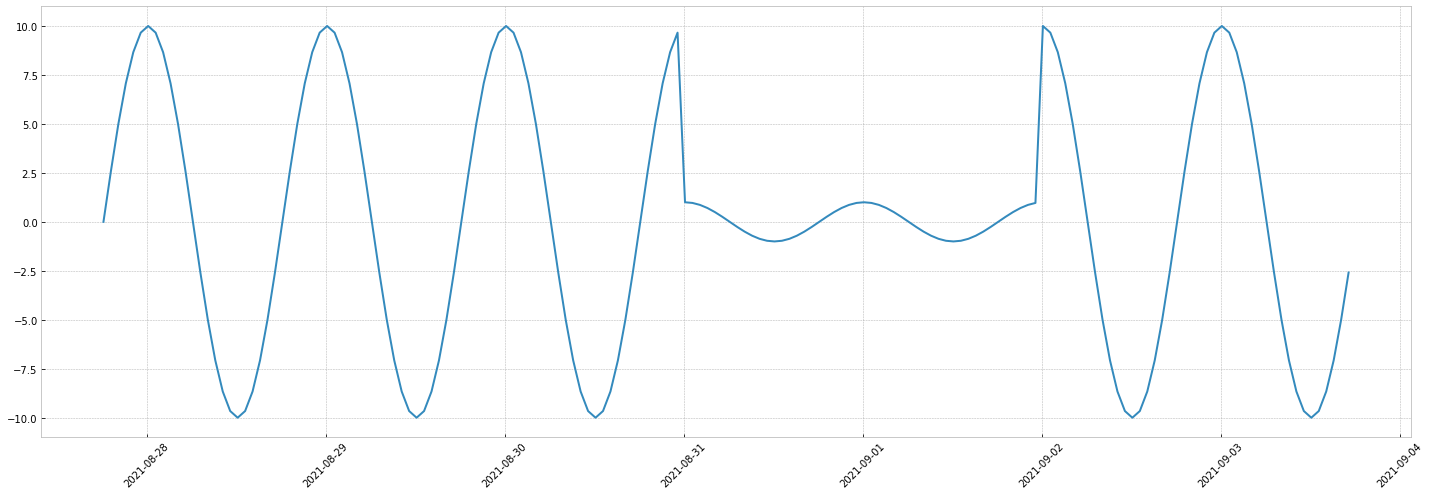
Thanks to signal combinations, this simple switch allows powerful simulations, for instance:

• the opening of a new shop adds a new constant value to the revenue of a company

from mockseries.trend import LinearTrend

previous_revenue = LinearTrend(coefficient=2, time_unit=timedelta(days=1), flat_base=100)

new_revenue = 2

revenue_signal = previous_revenue + (new_revenue * switch)

revenue_signal.preview_week()

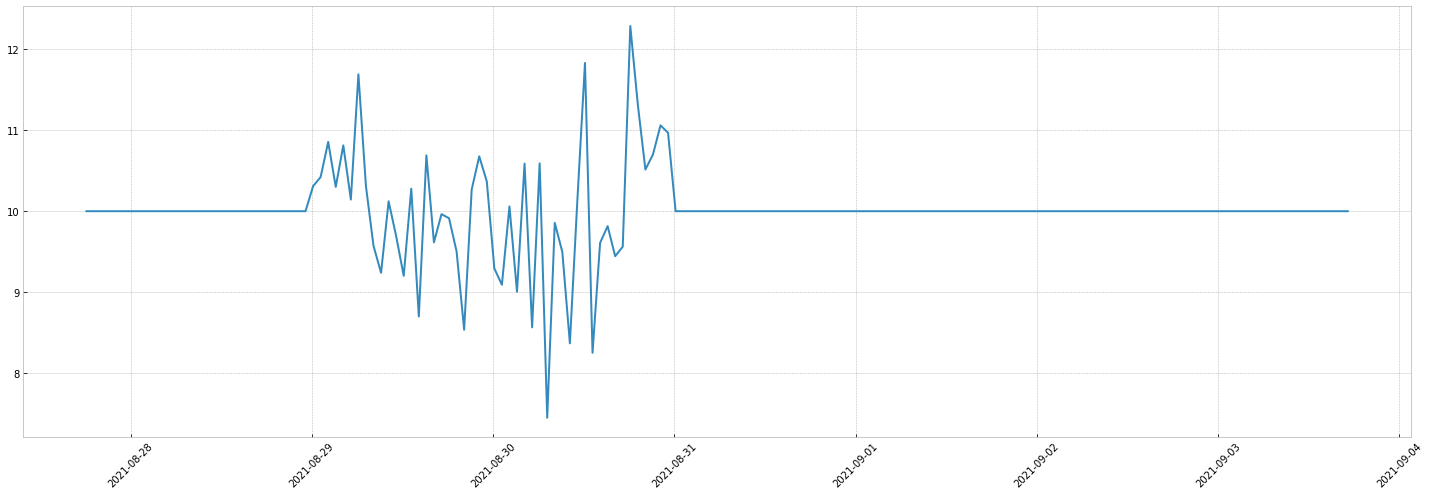
• a device gets broken, it generates noise, then is fixed:

from mockseries.noise import GaussianNoise

usual_device_value = 10 ## brodcasted to flat trend

noise = GaussianNoise()

signal_with_broken_device = usual_device_value + switch_and_revert * noise

signal_with_broken_device.preview_week()

• an outage results in a loss of 90% of a seasonal data volume.

from mockseries.seasonality import SinusoidalSeasonality

usual_volume = SinusoidalSeasonality(amplitude=10, period=timedelta(days=1))

outage_switch = Switch(

start_time=today_midnight + timedelta(days=4),

base_value=1,

switch_value=0.1,

stop_time=today_midnight + timedelta(days=6),

)

volume_with_outage = usual_volume * outage_switch

volume_with_outage.preview_week()

Transitions

For the moment, we've only seen instant transitions. This is the default behavior of the Switch.
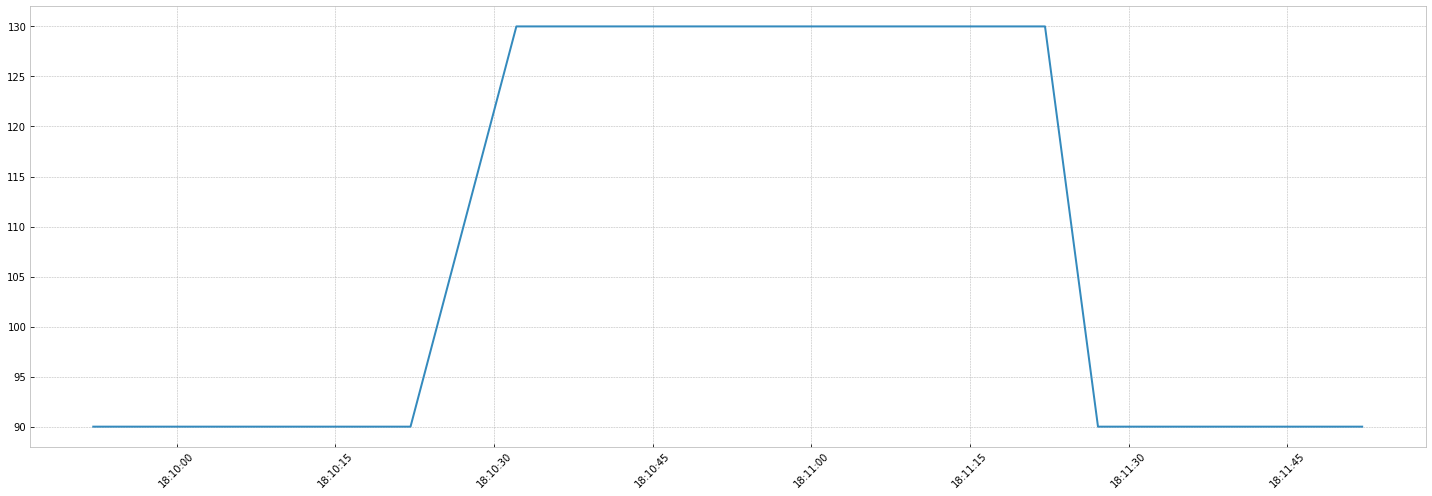
In real life, many change events have specific transitions behavior. Imagine you drive at 90km/hour, and you enter an highway: you change your speed to 130km/hour. At the end of the highway, you get back to 90km/hour. These changes are definitely not instant ! You accelerate: this is the transition.

A transition has:

• a window: for the car example, it's the time to change from 90 to 130k/hour
• a transition function: the shape of the change from 90 to 130km/hour (it most likely is not linear)
  Those depends on the car and the way you drive.

Linear transition

First, let's consider the acceleration of the car is linear.

The timeseries will be:

• car is at 90km/hour
• car accelerates linearly, it reaches 130km/hour in 10 seconds
• car is at 130km/hour
• car decelerates linearly, reaches 90km/hour in 5 seconds
• car is at 90km/hour

To implement this in mockseries, we pass a Transition object to the switch signal. The Transition describes the time and the shape of the transition.

from mockseries.transition import LinearTransition

linear_transition = LinearTransition(

transition_window=timedelta(seconds=10),

stop_window=timedelta(seconds=5),

)

now = datetime.now()

speed_switch = Switch(

start_time=now + timedelta(seconds=30),

base_value=90,

switch_value=130,

stop_time=now + timedelta(minutes=1, seconds=30),

transition=linear_transition

)

speed_switch.preview_minute(num_minutes=2)

Lambda transition

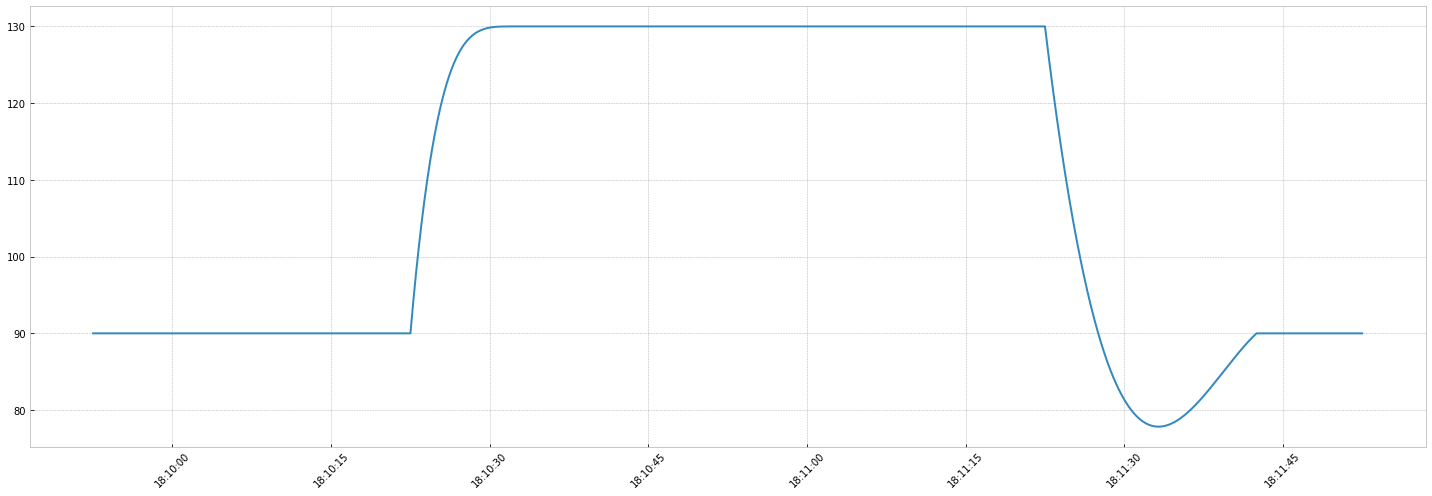
Above looks nice, but we want to use more complex transitions. The LambdaTransition allows to use custom transition functions.

The key idea of the lambda transition is that the transition behavior can be defined as a function such as $t(0) = 0$ (the very beginning of the transition) and $t(1) = 1$ (the end of the transition). This transition function is then rescaled to take into account the transition time and the base and switch values.
You just need a rough shape of the transition and define it on a [0-1] range.

Let's take the car example with:

• a perfect, smooth acceleration: accelerate a lot at the beginning then reach the new speed slowly
  $acceleration(x) = 1 - (1-x)**4$
• a brutal deceleration: decelerate too much, then get back to the base speed
  $deceleration(x) = 3.11111 * x^3 - 7.86667 * x^2 + 5.75556 * x$ (believe me for this one)

from mockseries.transition import LambdaTransition

acceleration = lambda x : 1 - (1-x)**4

deceleration = lambda x: 3.11111 * x**3 - 7.86667 * x**2 + 5.75556 * x

realistic_transition = LambdaTransition(

transition_window=timedelta(seconds=10),

transition_function=acceleration,

stop_window=timedelta(seconds=20),

stop_function=deceleration

)

now = datetime.now()

realistic_speed = Switch(

start_time= now + timedelta(seconds=30),

base_value=90,

switch_value=130,

stop_time=now + timedelta(minutes=1, seconds=30),

transition=realistic_transition

)

realistic_speed.preview_minute(num_minutes=2)

That's it! You now know how to:

• define switches
• define complex transitions

To go further:

• implement more realistic transitions function (checkout some automotive course)
• change the transition window size and see how it impacts the timeseries

Go to the next page to explore random switches. This is helpful to simulate random outages.